3.3 Isomorphic Graphs

Isomorphic Graphs

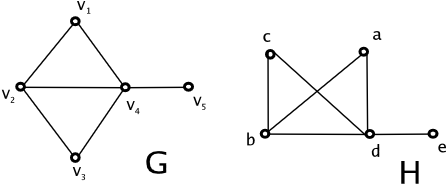
Graphs $G$ and $H$ look exactly the same with exception that their vertices and edges have different labels. $G$ and $H$ are not identical, but isomorphic.

Let $G$ and $H$ be simple graphs.
$G$ is isomorphic to $H$, denoted by $G\cong H$, if there exists a bijection $f:V(G)\to V(H)$ such that $uv\in E(G)$ if and only if $f(u)f(v)\in E(H)$

Graph Isomorphism Problem: Determine in polynomial time whether two graphs are isomorphic. (This is a very difficult problem that is still unsolved)

An unlabelled graph can be though of as a representative of an equivalence class of isomorphic graphs. We assign label to vertices and edges in a graph for the purpose of referring to them.